- Introduction:
In the vast world of mathematics, functions are fundamental tools for describing relationships between sets. Three key concepts in the study of functions are injective, surjective, and bijective functions. In this blog post, we will explore these concepts and understand their importance in the analysis of functions.
- Injective Function:
An injective function is one in which each element of the domain is mapped to a unique element in the codomain. In other words, different elements in the domain cannot have the same image in the codomain. Mathematically, if we have a function f: A → B, where A is the domain and B is the codomain, it holds that for every pair of elements x₁ and x₂ in A, if f(x₁) = f(x₂), then x₁ = x₂. Injectivity ensures that there are no duplicates in the mapping of elements.
- Surjective Function:
On the other hand, a surjective function, also known as an onto function, is one in which each element of the codomain has at least one corresponding element in the domain. In summary, no element of the codomain is left unassigned. Formally, if we have a function f: A → B, then for every element y in B, there exists at least one element x in A such that f(x) = y. Surjectivity ensures that no elements are "lost" in the mapping.
- Bijective Function:
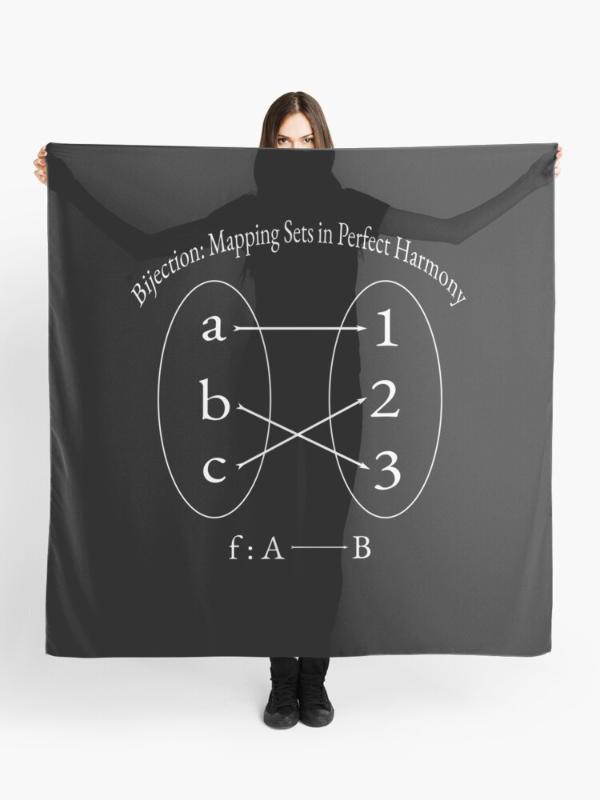
The third important concept is that of a bijective function. A function is bijective when it combines the properties of injectivity and surjectivity. In other words, each element of the domain is mapped to a unique element of the codomain, and each element of the codomain has a unique pre-image in the domain. If we have a function f: A → B, then for every pair of elements x₁ and x₂ in A, if f(x₁) = f(x₂), then x₁ = x₂; and for every element y in B, there exists exactly one element x in A such that f(x) = y. Bijective functions are particularly significant because they have an additional property: they have an inverse function that allows the mapping to be undone.
- Conclusion:
In summary, injective, surjective, and bijective functions are essential concepts in the study of mathematical functions. Injectivity ensures that each element of the domain is mapped to a different element in the codomain, surjectivity guarantees that no element of the codomain is left unassigned, and bijectivity combines these two properties, creating a one-to-one and reversible mapping. These concepts play a fundamental role in various areas of mathematics and other disciplines, such as set theory, functional analysis, and computer theory.
I hope this explanation has clarified the concepts of injective, surjective, and bijective functions. Thank you for reading!